Interest Rate Derivatives on Cardano

This post explains how we are implementing the Pricing and Risk Management of Forward Rate Agreements on the Cardano's UTXO model.

Table of Content

Context

A Forward Rate Agreement (FRA) is a type of Interest Rate Derivative used by financial intermediaries and large corporations to manage interest rate risk. FRAs are traded over-the-counter (OTC) and function similarly to Futures, which are traded on organized exchanges like the CME.

We are implementing FRA trading on the Cardano blockchain, primarily to automate the exchange of margin between counterparties. This automation enhances efficiency and reduces counterparty risk. More details on why this is important can be found in our earlier post here

Interest Rate Derivatives are a multi-trillion dollar daily market, with most trading between large financial institutions, corporations, and asset managers. Corporations use them to hedge their interest rate risk on loans, bond issuance, and other liabilities. Asset managers use them to express views on the direction of interest rates.

FRAs vs Futures

FRAs and Futures are very similar to each other, with the FRA being traded over the counter and the Futures having an organized exchanged. Differences and similarities between FRAs and Futures

• FRAs and Futures are very similar in settlement and collateral exchange. The main difference is that Futures have a standardized maturity schedule (Mar, Jun, Sep, Dec of each year ), whereas FRAs do not have a standardized maturity.
• FRAs are bilateral and not exchange-traded, blockchain can enhance transparency, reduce fraud, and ensure automatic settlement. Futures already have clearinghouses mitigating counterparty risk.
• FRAs are tailored contracts, leading to complexities in settlement. A blockchain can standardize and automate settlement through smart contracts. Futures are standardized and benefit less from blockchain for individual contract settlement.
• Implementing blockchain for FRA settlement can demonstrate its benefits in OTC markets before tackling more complex and highly regulated futures markets. Exchanges already have efficient settlement mechanisms for futures, making blockchain an incremental rather than transformative improvement.
• Given their similarities, the price of FRAs can be derived by calibrating an interest rate curve from the prices of Futures. Similarly the risk parameters can also be estimated from the price dynamics of Futures

Contract Terms in a FRA

When two parties trade an Interest Rate FRA, they enter into a contract to fix an interest rate for a specified Notional amount over a future period.

FRAs are cash-settled at maturity, meaning that there is no exchange of Notional amount at the start, nor at the end of the contract. The difference between the contracted rate and the rate prevailing in the market at maturity is settled on a net basis

The two parties agree on:

• Notional Amount (N) - The amount in USD on which interest is calculated (though no actual exchange of principal occurs at the start, nor at maturity).
• Contract Rate (f) - The fixed interest rate agreed upon in the contract.
• Reference Rate (rt) - A floating benchmark rate (e.g., SOFR). This is the reference interest rate at maturity of the FRA. Prior to maturity these are market interest rates calibrated from market data for standard tenors (e.g. from Futures) and interpolated to for the remaining tenor of the FRA contract.
• Settlement Date - A date in the future when the FRA is settled.
• Contract Period (CP) - The period over which the interest rate is measure (e.g. 90 days for 3-month SOFR)

The day count convention is 30/360 which means that each month is 30 days and a year is 360 days.

Settlement Process

Settlement happens at maturity and Posting of margin during the life of the contract prior to maturity. The posting of margin is sometimes referred to as "exchanges of collateral". The settlement amount needs to be calculated for both of these events and is give by:

This settlement amount is from the point of view of a buyer (borrower) who locks into a borrow rate f . For the other party the Settlement amount is symmetrical and is given by

The remaining formulations in this article are symetrica for a buyer and seller of FRA with the St by default being shown from the side of the buyer (borrower)

Settlement at Maturity

At the maturity date, the actual market reference rate (e.g., 3-month SOFR) is compared to the agreed Contract Rate f. The difference determines who makes a payment to whom.

• If the market reference rate exceeds the agreed Contract Rate then the the buyer of the FRA (who agreed to pay a fixed rate) receives a payment from the seller.
• If the market reference rate is lower than the agreed Contract Rate. The seller of the FRA receives a payment from the buyer.

Posting of Margin

To ensure that one of the counterparties does not walk away from their obligation if the market turns against them, the two parties exchange margin throughout the life of the contract.

The posting of margin requires the Settlement amount to be calculated based on prevailing market interest rates rt.

The amount of margin to post is a combination of:

• Initial Margin (IM), which relies on the risk sensitivity of the FRA contract and the Risk Parameter that is calculated by the Risk engine. IM is the same amount for buyer and seller of a FRA

Where the risk sensitivity is given by

• Total Margin (TM) - which is also sometimes referred to as Margin Requirement - is the difference between the Settlement amount St and the Initial Margin IM

The IM is posted at the start of the contract and the TMt is checked periodically and determines if additional margin will need to be posted, or if any margin can be withdrawn.

The party needs to have enough margin posted into the smart contract to exceed the Total Margin Requirement. Failure to have enough margin posted to the smart contract by the end of the day, grants the other party the right to terminate the contract and keep all margin that has been already posted to the smart contract by both parties.

• If TM < 0 then margin needs to be posted by the party into the contract to at least that amount. This number can fluctuate from day to day and needs to be monitored by both the buyer and the seller.
• If TM > 0 then the expected Settlement amount is greater than the Initial Margin and margin can be withdrawn from the contract. This case occurs when the the Settlement amount is greater than the Initial Margin requirement

kt is the risk threshold that is interpolated from calibrated risk threshold curve K and is given by:

The K is determined by calibrating the volatility of the interest rates from history and adding a conservative factor on top. This is further detailed in the Risk Engine section below

Oracle

The Oracle stores the market interest rate Rt and the Risk parameters Kt at standard tenors. These are calibrated from the markat prices and historic price dynamics (volatility) of Futures.

The Oracle design is aligned with the design adopted by Charlie 3 and has the following characteristics

• The oracle is a smart contract and has an address on the Cardano blockchain
• The market data is stored in a UTXO at the smact contract's address as an Inline Datum
• Other smart contract can read the content of this Inline Datum
• A unique NFT is stored at the UTXO, letting anyone who consumes the information in the Inline Datum that the information is genuine
• Only 1 authorized wallet can consume UTXOs from the smart contract
• Updates to the market data are performed by consuming an existing UTXO and creating a new UTXO at the same address with updated market data in the Inline Datum

Oracle Smart Contract

Sample Aiken code for the Oracle:

validator oracle {
  spend(
    datum: Option<Datum>,
    redeemer: Redeemer,
    _own_ref: OutputReference,
    tx: Transaction,
  ) ->  Bool {
    
    list.has(tx.extra_signatories, #"05ffe34a7ded67d3f4c11113b909f8f9313bcf352fa3aa887c51ca90")

  }

}

The smart contract has the address:

addr_test1wqzdedqpy2ljhf70dw89p399z836dvmgs7sn6qyr0gndu7gp9k7en

Link to the oracle address on a blockchain explorer LINK

Oracle Updated Transaction

When the oracle is update, it consumes an existing UTXO at the smart contract and creates a new UTXO with the updated market rates. Example of this transaction is shown in the printscreen below

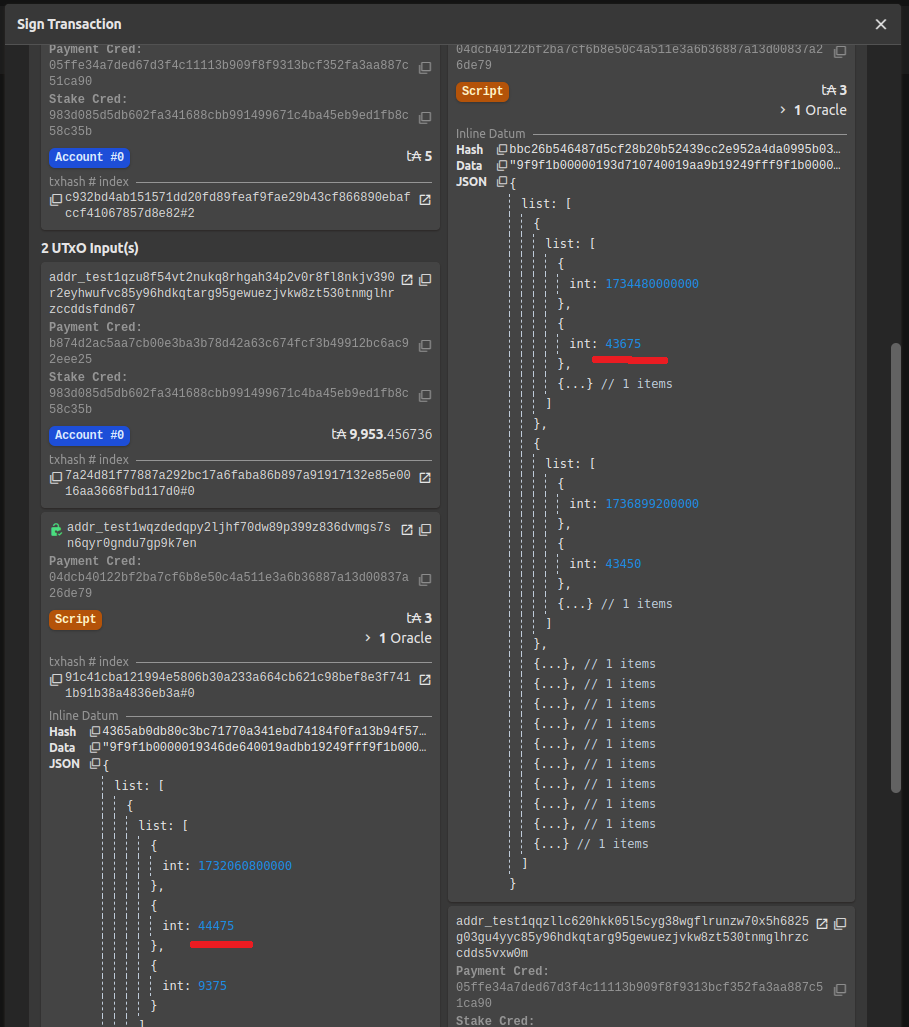
This update transaction can be viewed on the blockchain explorer: https://preview.cardanoscan.io/transaction/c86a67c2b2b387dff5a276fdcbc904e92c0aa80a8ae75685daeac6279382b884

Market Data Design

The market data is encoded as an interest rate curve of forward rates, expressed as annualized % with a 360 day count.

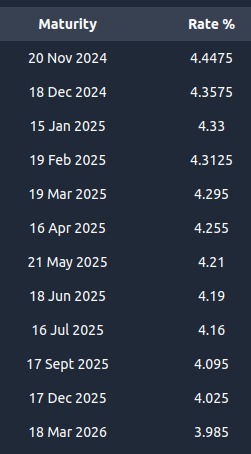
The market interest rates are calibrated using the prices of Futures that are traded on the CME Exchange

Market Data Encoding On-Chain

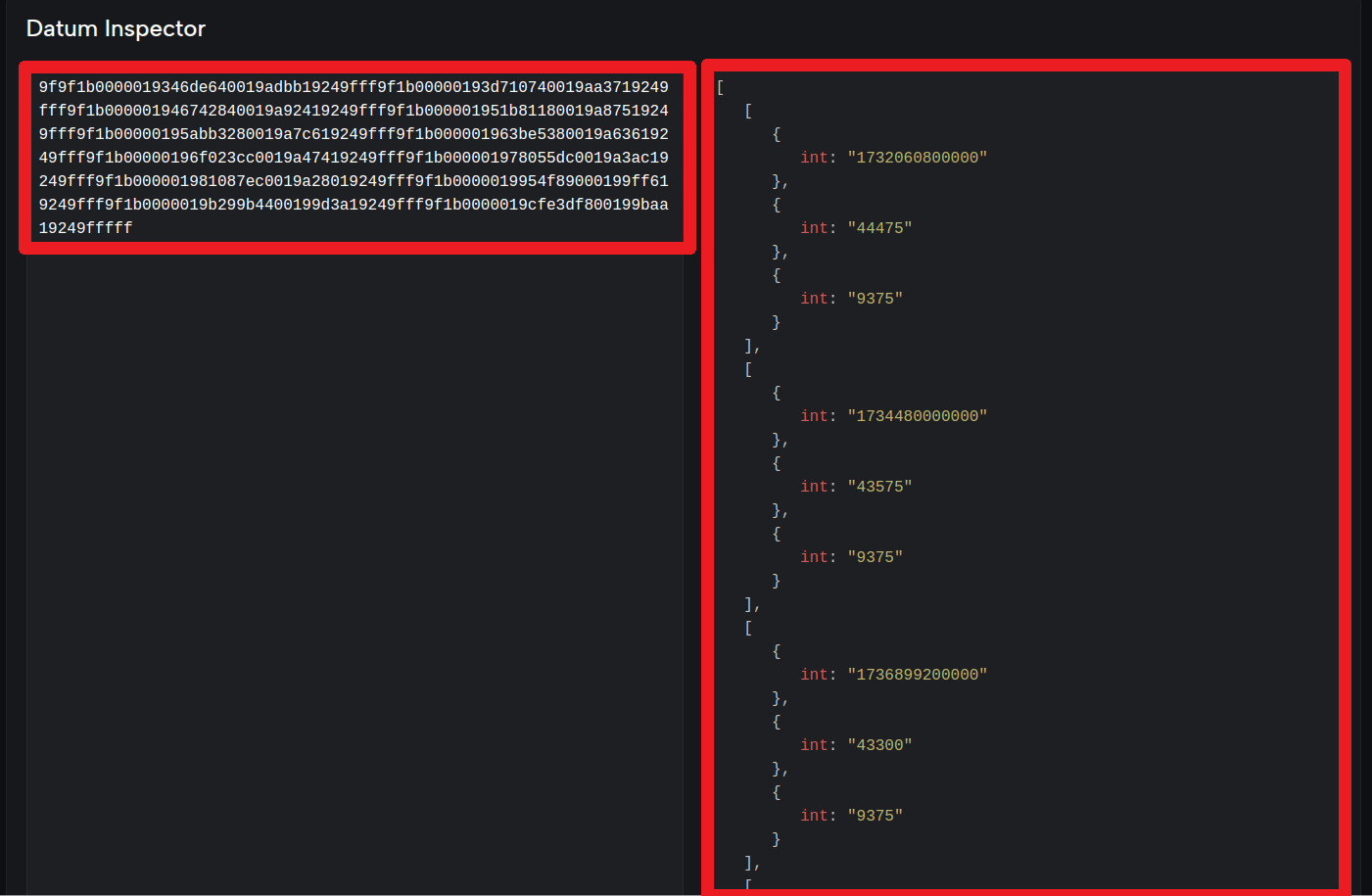
The market data is stored at a UTXO as an Inline Datum. The data is organized as a "list" of "lists" with the following elements

• Maturity of the Forward Interest Rate, converted into a Unix timestamp in milliseconds and encoded as an integer.
• Forward Interest Rate encoded as an integer. The interest rate is multiple by 10,000 and truncated. This gives 4 decimal points of precision
• Risk Parameter encoded as an integer. The risk parameter is multiple by 10,000 and truncated. This gives 4 decimal points of precision

Oracle NFT

The Oracle NFT confirms that the market data at a UTXO is genuine. This NFT sits at the same UTXO as the where the Market Data is stored in the Inline Datum and a smart contract that reads this market data will check if this particular NFT is present at that same UTXO.

The Oracle smart contract imposes that only a wallet with a Public Key Hash 05ffe34a7ded67d3f4c11113b909f8f9313bcf352fa3aa887c51ca90 can consume UTXOs at the Oracle address. No other wallet can retrieve the Oracle NFT from the Oracle address.

This functionality prevents a malicious actor from writing incorrect market data, as it would not have the correct Oracle NFT attached to the UTXO and therefore other smart contract that rely on this market data would discard it.

Pricer

The price gives the market value of the FRA contract at any point in time from inception until maturity. At maturity the Settlement amount of the FRA is given by the Settlement formula

The price of the FRA prior to maturity is also given by the Settlement formula, however the input for the Reference Rate is an interpolated rate from Market Rates (rather than the Reference Rate)

The Price of the FRA is the discounted value of the Settlement amount and is given by the following formula:

Interpolating the Market Rate

The interpolated market rate rt is given by the following formula for a given FRA tenor t

Risk Engine

The risk engine is responsible for estimating the amount of margin that is required to cover potential price changes of the FRA over the course of 2 days. It is used as an input into the Initial Margin IM formula. To calibrate this amount, we used the historic price volatility of Futures.

The parameter is expected to remain static for extended period of time unless a large increase in volatility is observed in interest rates that exceeds the volatility that prevailed over the previous 4 years.

The parameter should be updated if on any consecutive 2 day period the interest rate moves by more than the previous maximum of 62.5 basis points.

Risk Parameter

The risk parameter is the maximum interest rate move over a 2 day period. It is calculated as the largest 2 day interest rate move from a sample of 6 SOFR futures contracts over the period from May-2021 to Jan-2025

The table above shows that the maximum 2 day move was 0.625 percentage points. We add a conservative factor of 50% on top to further reduce the probability of a market move exceeding this threshold.

To make this parameter flexible to be changed through governance in the future we made two design choices:

• The parameter is encoded in the Oracle together with the market interest rate. This ensures the parameter is written on the blockchain and can be consume by Cardano smart contracts and web interfaces
• The parameter is encoded alongside the interest rate tenors in the Oracle. This makes it possible in the future to make the risk parameter granular to individual tenors. We did not observe material variance in the largest market moves between different futures for the current calibration of the parameter (as can be seen in the table above)
• The parameter update could be further automated in the future by reading the 2 day history from the oracle price history and updating when a new maximum 2 day move is observed

Implementation

The functionality described in this article are implemented at:

Block Margin

Interest Rate FRAs on the Blockchains